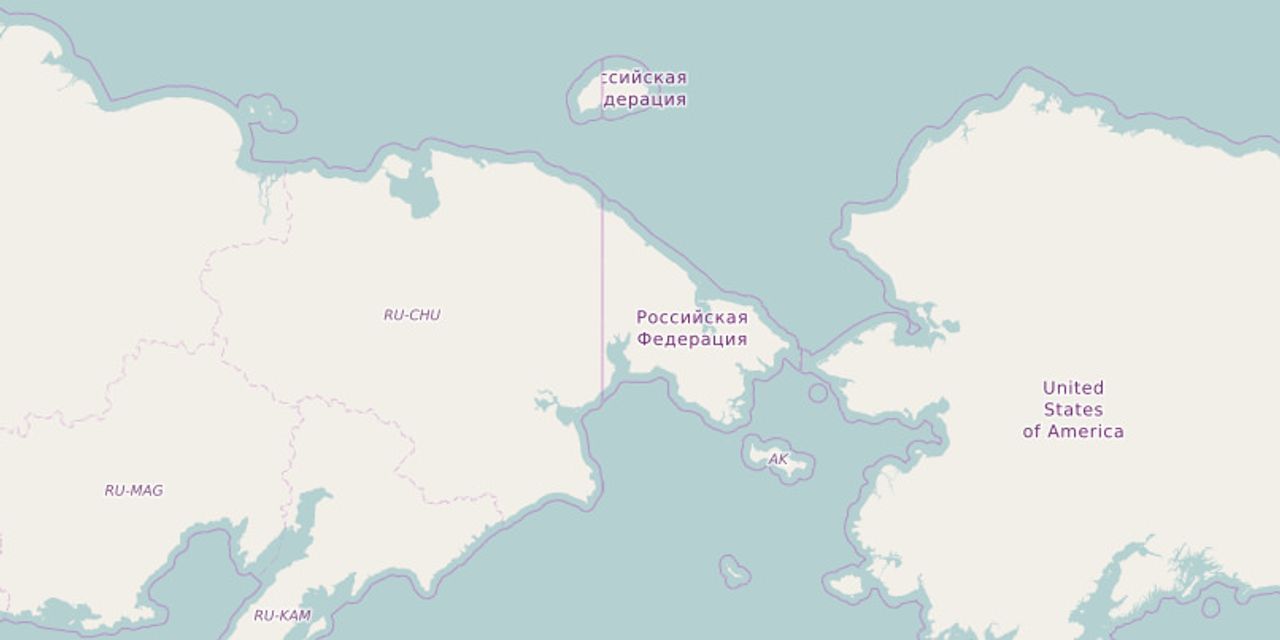
The 180th Meridian
Crossing through Russia, Fiji, Antarctica, two seas and three oceans, the 180th Meridian is a geometric wonder and a persistent problem in geography and technology. It's interwoven with problems of projection, interpretation, and interface. It's the reason there's a line through Russia on some maps. You might have already grappled with the nasty 180th and want to know the full story. Anyway, let's begin.
Basics & Assumptions
- Geographic positions are often stored as numbers: longitude and latitude, represented as degrees spanning from -180 to 180 longitude and -90 to 90 degrees latitude. On a typical world map, -180 longitude is the line at the far left of the map, left of the Americas, and 180 longitude is at the far right, right of Russia, China, and Australia.
- In this article, I will put longitude first.
- On top of a map, you have data: geometric shapes including points, lines, and polygons. Points are identified just by a longitude, latitude pair. Lines are a list of longitude, latitude positions. Polygons are also lists of longitude, latitude positions in loops.
- Amongst the many things you'll want to put on a map are trips, like flight paths, that can circumnavigate the globe and cross the 180th meridian.
- Some software treats longitude values outside of the range of -180 to 180 - like
longitude=300as invalid.
The Problem
How do you represent a line that cross the 180th meridian? How do you represent a polygon that overlaps with the 180th meridian?
One step deeper.
Let's say you have a line with two coordinates:
- Longitude -0.12119, Latitude 51.51727
- Longitude -1.92913, Latitude 52.47556
Intuitively, these places are close to each other. The first is London, the second is Birmingham. If you were asked to draw a line between the two, it'd probably look like this:
The direction from the first point to the second is North and East. If you want to find a place between these two, you'd average the numbers:
- (-0.12119 + -1.92913) / 2 = -1.02516 Longitude
- (51.51727 + 52.47556) / 2 = 51.996415 Latitude
That's somewhere else in England, roughly between the two places, not of note, it's probably quaint but it's irrelevant.
A conclusion to draw: when places are close to each other and far from the 180th meridian, the line between them seems obvious and everything is easy.
Let's try an example close to the 180th Meridian.
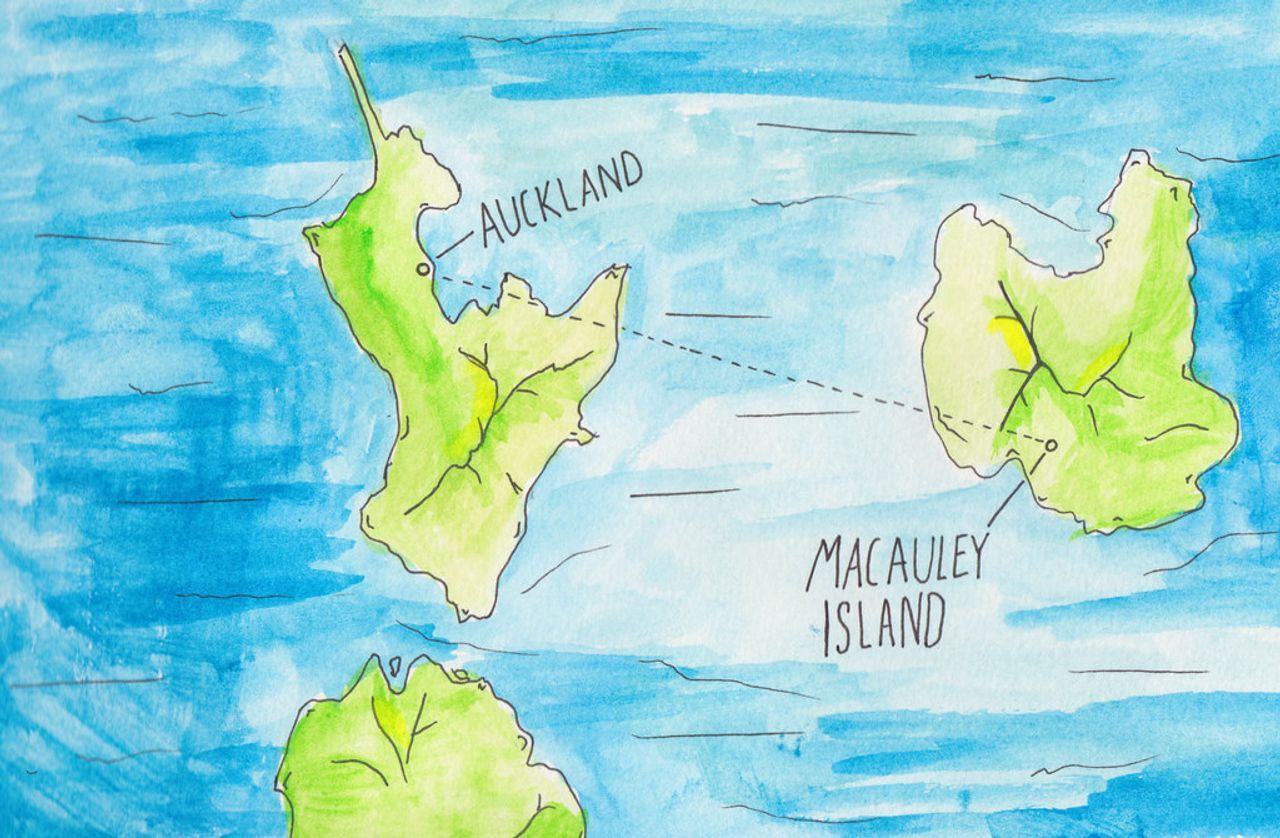
Not to scale or accurately drawn. So inaccurately, in fact, that MacAuley should be north of Auckland. But it was fun to watercolor.
- Longitude 174.76398, Latitude -36.85496 (Auckland, New Zealand)
- Longitude -178.43054, Latitude -30.23261 (Macauley Island, also a part of New Zealand)
If you were to draw a line between these two places, you have two options: go 'all the way across', or jump across the 180th meridian. If you were to find a point between them using a simple average,
- (174.76398 + -178.43054) / 2 = -1.83328 Longitude
- (-36.85496 + -30.23261) / 2 = -33.543785 Latitude
That's in northern Algeria, half a world away from either place.
As humans, going the long way doesn't seem right: the shortest path is common sense. That's the assumption that we'd use in real life: if my friend was traveling from Baltimore to Washington, DC, I'd assume they would drive 45 miles down the highway, instead of flying around the world.
The problem with intuitive guessing with angles, a parable
Someone shows you a coin in their hand, head side up. They turn around, flip the coin, and show you the coin again, head side up again. How many times did it flip?
You have no earthly way of knowing.
The angle of the coin in the person's hand isn't an absolute number that keeps getting higher the more times it flips. No, every time the coin goes around 360 degrees, it's in the same place again.
Similarly, when you perfectly execute a 720 double kick-flip on your skateboard or more likely in a video game, you end up where you started off: the skateboard is facing forward. If your friends missed your accomplishment, everything's the same.
Back to the issue at hand: how do we represent features that cross the 180th meridian?
Attempting intuition
You could try to write software that guesses whether -179 and 179 are trying to hop to each other: essentially simulating human judgment. Some software tries to do this, and occasionally it'll meet people's expectations. Apple, in fact, has this behavior in parts of MapKit.
But it has real downsides: identifying hops across the 180th is tricky and opinionated. And once you create some 'magic' behavior that automatically connects lines that wouldn't be connected usually, it becomes harder to represent the case where someone does, for some unfathomable but very possible reason, want to represent a flight path the long way from New Zealand to another island in New Zealand.
Using longitudes above and below 180 and -180**
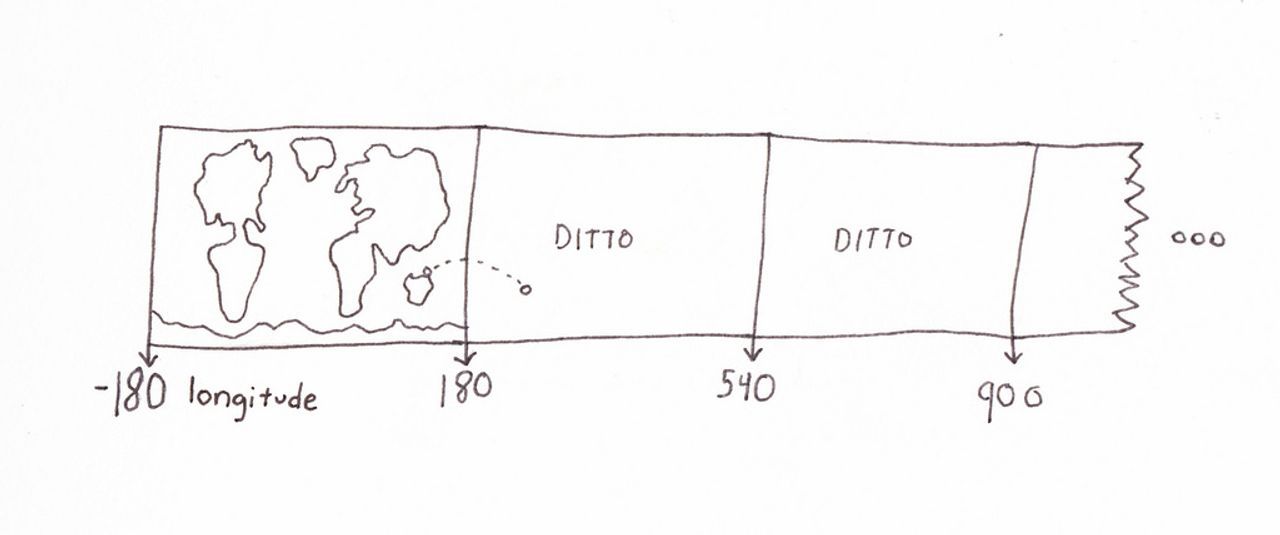
This has been my personally preferred approach for years. For example, if you want to travel east from Auckland to Macauley Island, instead of going from 174.76398 to -178.43054 longitude, you would travel from 174.76398 to 181.56946: two numbers that are nicely, mathematically, close to each other. To do this, you add or subtract 360 degrees from one of the numbers until it's close to the other number on the number line.
There's a downside, and it's not just that 200+ longitude values look weird. Many of the programs and libraries that work with geographic data will happily show 180th-meridian-crossing geometries represented this way, but some reject values outside of the -180, -90, 180, 90 box, either clipping and hiding them or failing entirely to avoid undefined behavior.
Splitting lines and polygons that cross the 180th into two
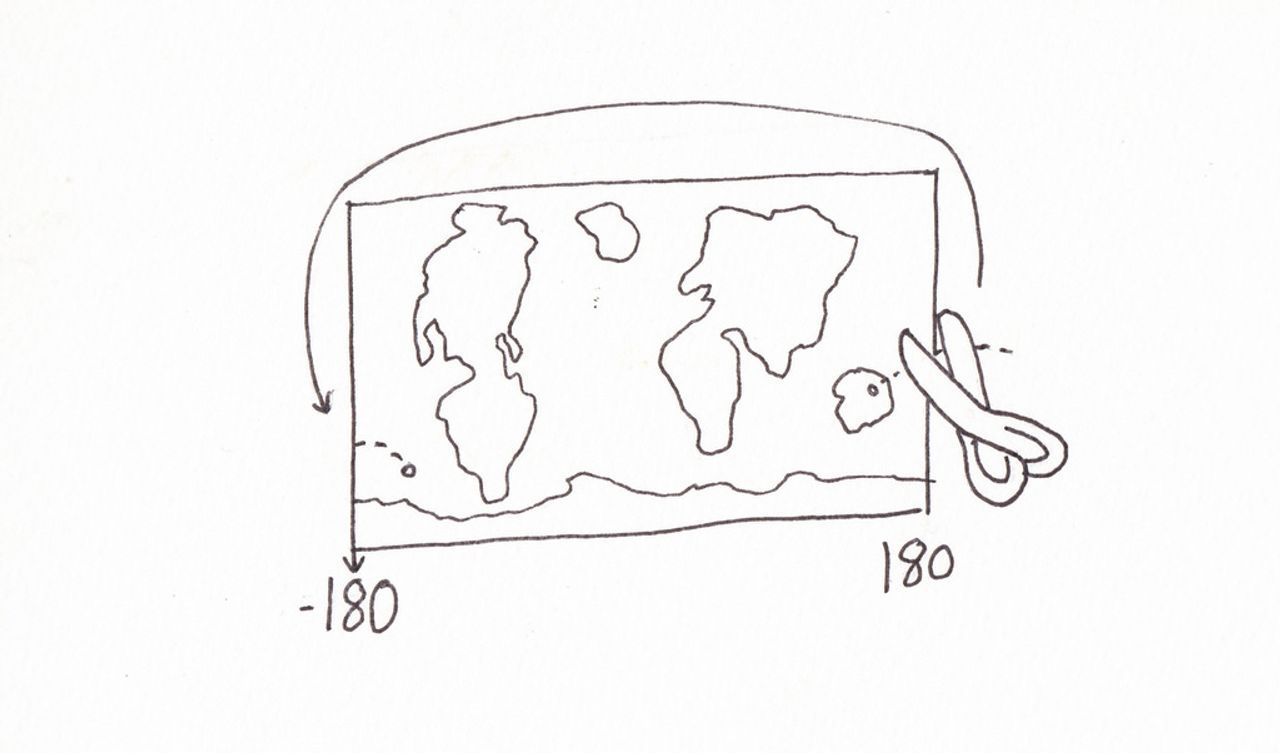
This is the approach that you might have seen on OpenStreetMap from earlier - the reason why Russia has that unsightly line on OpenStreetMap running right through it.
The gist is: given a geometry that passes through the 180th meridian, slice and cut it until you have multiple geometries that don't cross the meridian. In GeoJSON and many other formats, you can use multipart geometries like MultiLineString and MultiPolygon to split up geometries without duplicating information about the features they describe.
This, in fact, is the GeoJSON spec recommended solution:
In representing Features that cross the antimeridian, interoperability is improved by modifying their geometry. Any geometry that crosses the antimeridian SHOULD be represented by cutting it in two such that neither part's representation crosses the antimeridian. - GeoJSON Spec, 3.1.9
Unlike the other solutions, this one is both free of 'magic' or intuition, and also safe: there's no chance that this encoding will be rejected or misinterpreted by other software. So it's easy to interpret correctly, and safe.
But there are two relevant downsides:
The 'crease' problem. Cartographic software usually draws MultiLineString and MultiPolygon features exactly the same as layered LineStrings and MultiPolygons. So if you have to split your lines and those lines have beginning & ending marks, or you split a polygon and it has a border, there might be a border in the final rendering.
Splitting lines isn't obvious. Well, it can seem obvious: to find the midpoint in degrees, you can offset one coordinate by increments of 360 until it's close on the number line to the other, find the angle between the two, and then the distance from the eastern-side point to the 180th meridian will be the bottom or top of a right-angle triangle, and you do the high-school trig to get there. Remember SOHCAHTOA.
But is the midpoint in longitude, latitude correct? In many cases, it isn't.
If you were displaying your map in the Equirectangular projection, it would look right, but few people use that projection. It's nice in that it's directly related to longitude & latitude, but fails in most other cartographic aspects.
If you're displaying your map in the Web Mercator projection (you probably are) and splitting a line at its midpoint by using longitude and latitude, you're going to get a curved line, unless the latitude of the position on one side is exactly the same as the latitude on the other. With short lines, the curviness won't be very noticeable, but with longer ones it will be.
Conclusions
The GeoJSON Spec-recommended technique is probably the best way to go. It puts more responsibility in the hands of data producers and avoids any possibility of invalid data. But it's not inherently easy to implement - if you're dynamically adding a line to a web map through Leaflet's GeoJSON layer type, calculating the split point through the 180th meridian is tricky. A library will likely crop up that contains that complexity.
Regardless of the spec's recommendation, it's likely that the 180th will pose a challenge for mapmakers into the future, regardless of specific technology choices. Longitude and latitude as a means of storing information is a deeply-set assumption for most geography, and the translation of places on a rotating 3D globe into numbers and pictures will always be imperfect and fraught.
Post-conclusions
Careful readers may glean an idea from the coin flip example: I said that you can't tell how many times a coin has flipped, since its angle is an absolute number, not a number relative to the old position.
Most geospatial formats store coordinates in absolute form: each coordinate is recorded in full, so it is encoded as, for instance, -72, 24, whether that occurs as a point or as one of the positions in a line.
There is another way: delta encoding, or 'relative encoding'. With delta encoding, instead of storing each coordinate with absolute numbers, you store the absolute position of the first position in, say, a line, and then store deltas - changes - from that position. For instance, if a line started at -72, 24, instead of storing:
- -72, 24 to
- -73, 22 to
- -77, 20
You'd store
- -72, 24, and then move by
- -1, -2, and then move by
- -4, -2
This somewhat dodges the -180 problem, since a line that crosses the 180th meridian could be encoded as:
- -179, 24, and then move by
- -2, 0 (and this ends up at
179, 24)
That is, you're storing a line as a series of vectors, rather than a series of absolute positions. Since the vectors have direction, you know if you're going a short hop across the 180th, or the long way.
Which would be great, except that there are some disadvantages to delta encoding:
- You can't read or modify an arbitrary coordinate in a line or polygon, since it's relative to all of the coordinates before it, and all the coordinates after it will be affected
- This encoding is clever but unpopular: you'll need to convert to and from encodings often, so lowest-common-denominator characteristics win out, every time.
There are instances of delta encoding - Mapbox Vector Tiles and TopoJSON both use the technique - MVT is a presentational format and TopoJSON mainly uses it as an efficiency win, rather than an actual functional difference.
FAQ
- Isn't that called the International Date Line? Not quite. The International Date Line has a lot of overlap with the 180th Meridian, but it's not a straight line. It squiggles so that Russia and Fiji are entirely on one side and other island formations aren't divided by the line.
- Why is the 180th meridian where it is? Well, the focus has always been on the Prime Meridian, which moved around until it finally centered on Greenwich when Sir Airy modestly chose his town to be the center of the world.
- What about local datums? (For the uninitiated, there are ways other than longitude and latitude to represent places on Earth - basically mini systems of measurement that could measure feet from some reference point in a town, rather than degrees over the whole world). Okay, so, yes! There are datums that straddle the 180th, and thus let you cleanly save things that cross it. But local datums are, as the name specifies, local: they can't usually be applied to the whole world in any kind of meaningful way, so they aren't terribly popular in the world of new software which is usually global-first.
- Have a question or found a mistake? Hit me up on twitter @tmcw
- Wondering how the trigonometry solution for cutting lines at the 180th works? Stay tuned for tomorrow's episode.
@macwright.com on Bluesky, @tmcw@mastodon.social on Mastodon