Math keeps changing
This is a written version of a talk that I gave at WaffleJS in February, which itself was an expansion of a Twitter conversation from October.
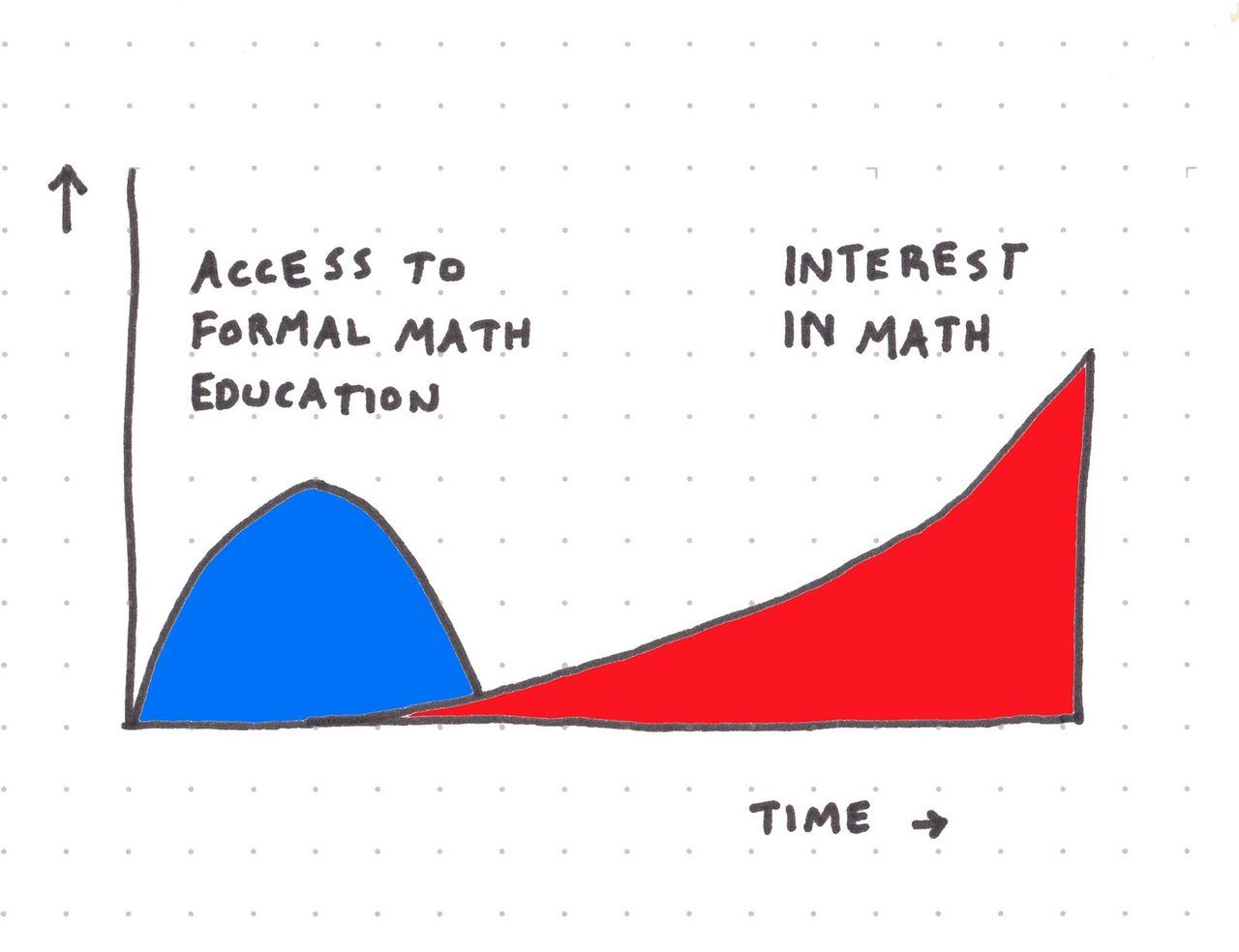
Okay, so it starts with my delayed math education. As part of my Computer Science program, I had access to world-class math professors, access that I mostly wasted. I didn't like math: the topics were so removed from practice, and I was already frustrated by the highly theoretical, and -- I thought at the time and mostly still do -- out-of-touch CS program.
Unfortunately, a few years after graduating, I got the hunger for math. Seeing how I could apply just a little bit of math knowledge to great effect in my work & hobbies had me inspired. But I had no clear way of learning it.
So I started Simple Statistics in 2012 as a way to learn math, and ever since then, I've expanded and maintained the project. It now includes a lot of different algorithms, is one of the most 'starred' JavaScript math projects, and presumably is used by people.
But I started it in 2012. In tech years that's a really long time ago. Between then and now, there have been 8 LTS releases of Node. JavaScript and its environments have radically changed. 2012 was before the introduction of React or the first commit to Babel.
So what I noticed over the years was that tests kept breaking when I updated Node. I'd have a test like:
t.equal(ss.gamma(11.54), 13098426.039156161);That would work in Node v10 and break in Node v12. And this is not some complex method: gamma is implemented with arithmetic, Math.pow, Math.sqrt, and Math.sin.
Arithmetic
So I know what you might be thinking: arithmetic. JavaScript, on Twitter, gets a lot of heat for this behavior:
0.1 + 0.2 = 0.30000000000000004
As I wrote in JavaScript wats, dissected, this is the behavior of every popular programming language, even stodgy pedantic ones like Haskell. Floating point arithmetic might be weird, but it's very consistent and well-specified: the IEEE 754 specification is rigorously implemented. So it's not arithmetic: addition, subtraction, division, and multiplication are pretty set in stone.
Math
What it was, was Math. In particular, all of the methods that come after Math.
Methods like Math.sin, Math.cos, Math.exp, Math.pow, Math.tan: essential ingredients for geometry and basic computation. I started isolating changes in basic function behavior between versions. For example:
Calculating Math.tanh(0.1)
// Node 4
0.09966799462495590234
// Node 6
0.09966799462495581907
Calculating Math.pow(1/3, 3)
// Node 10
0.03703703703703703498
// Node 12
0.03703703703703702804
To make matters worse, it's not just Node's behavior that's changing: so are browsers and other places you use JavaScript.
So this led to the question: what is math?
Trigonometry methods are easy to show: given a unit circle and a few months of high school, you know that cosine and sine will get you coordinates on the rim, and that they'll draw little squigglies if plotted on X & Y. Actually deriving those methods is what you'll learn in advanced classes, but the method that you use - the Taylor series - relies on an infinite series, which would be rather laborious for a computer to solve.
"There is no standard algorithm for calculating sine. IEEE 754-2008, the most widely used standard for floating-point computation, does not address calculating trigonometric functions such as sine."
Computers use a variety of different estimations and algorithms to do math, things like CORDIC and various cheating algorithms and lookup tables. This heterogeny explains all of the 'fastmath' libraries you can find on GitHub: there's more than one way to implement Math.sin. Famously, Quake III Arena used a faster replacement for the inverse square root method in order to speed up rendering.
So math is implemented as algorithms, and there are multiple common algorithms – and variations of those algorithms – used in practice.
Instead of telling implementations to pick an algorithm, the JavaScript specification grants them a lot of wiggle room in terms of how they implement these basic functions.
The behaviour of the functions acos, acosh, asin, asinh, atan, atanh, atan2, cbrt, cos, cosh, exp, expm1, hypot, log,log1p, log2, log10, pow, random, sin, sinh, sqrt, tan, and tanh is not precisely specified here except to require specific results for certain argument values that represent boundary cases of interest.
-ECMA-262, 10th edition, section 20.2.2 aka "JavaScript"
I don't know the inner workings of the standards committees, but I imagine they wanted to make sure that just in case Intel or AMD introduce super-fast new math instructions in a new processor, JavaScript wouldn't have a compatibility crisis.
Because there are a lot of JavaScript interpreters that are commonly used, because JavaScript is often used via web browsers and there still is some competition between web browsers, and because even popular JavaScript implementations are under pressure to evolve quickly to be the most performant… because of all that, this matters. You actually will encounter, on a regular basis, differences in math.
This doesn't matter as much in other interpreted languages, because they tend to have 'canonical' interpreters: most of the time you use the Python interpreter of the Python language.
Where math happens
Next let's zoom into where these math implementations live. See, in JavaScript, there are three places where basic math can happen:
- The CPU
- The language interpreter (the C++ and C code that underlies JavaScript implementations)
- In software itself, as a library
1: The CPU
This was my first guess: I assumed that since CPUs implement arithmetic, they might implement some higher-level math. It turns out that CPUs do have instructions to do trigonometry and other operations, but they're rarely invoked. The CPU (x86) implementation of sine doesn't get much love because it's not reliably faster than an implementation in software (using arithmetic operations on the CPU), nor as accurate.
Intel also bears some blame for overstating the accuracy of their trigonometric operations by many magnitudes. That kind of mistake is especially tragic because, unlike software, you can't patch chips.
2: The language interpreter
This is how most of the implementations do it, and they implement math in a variety of ways.
- V8 & SpiderMonkey use (slightly different) ports of the fdlibm library for most operations. It has been passed down through the generations, originally written at Sun Microsystems.
- JavaScriptCore (Safari) uses cmath for most operations.
- Internet Explorer used some cmath, but also used some assembly instructions and actually did use CPU-provided trig methods when it was compiled for CPUs that had them.
Historically, all of these implementations have shifted: V8 used to use a homegrown solution for math, and then used a port of fdlibm to JavaScript, before finally settling on fdlibm in C.
Why this is an issue
Here's why this is a problem: it chips away at JavaScript's ability to give consistent results to any problem including mathematics. And that especially hits data science. I want JavaScript to be a contender for data science in the browser, and – amongst some other issues, like number types and a confounding lack of a commonly-used data-frames library – an inability to produce replicable results means adding more crisis to the replication crisis in the sciences.
The third way
There is a way out that we can use today. stdlib is a JavaScript library that reimplements higher-level math using arithmetic alone. Arithmetic is fully-specified and standard, so the results that stdlib gives you are also fully consistent, across all the platforms.
This comes at the cost of complexity and speed: stdlib isn't consistently as fast as built-in methods, and you'll need to require a library 'just' to compute sine.
But in the wider view, this is pretty normal! WebAssembly, for example, doesn't give you higher-level math methods at all and recommends you include a math implementation in your modules themselves:
"WebAssembly doesn’t include its own math functions like sin, cos, exp, pow, and so on. WebAssembly’s strategy for such functions is to allow them to be implemented as library routines in WebAssembly itself (note that x86’s sin and cos instructions are slow and imprecise and are generally avoided these days anyway)."
And this is the way that compiled languages have always worked: when you compile a C program, the methods you import from math.h are included in the compiled binary.
Using an epsilon
If you don't want to include stdlib to do math but you do want to test math-heavy code, you'll probably have to do what simple-statistics does right now: use an epsilon. Of the 5+ uses of epsilon in math, the one I'm referring to is "an arbitrarily small positive quantity". It's a tiny number. Here's simple-statistics's implementation: the number 0.0001.
You then compare Math.abs(result - expected) < epsilon to make sure you got within range of the desired value, with a little bit of wiggle room.
The moral of the story
Here's where I was a little short on time in person and have some room to expand.
First, what's under the hood is rarely what you expect. Our current tech stack is heavily optimized and a lot of optimizations are really just dirty tricks. For example, the number of hardware instructions it takes to solve Math.sin varies based on the input, because there are lots of special cases. When you get to more complex cases, like 'sorting an array', there are often multiple algorithms that the interpreter chooses between in order to give you your final result. Basically, the cost of anything you do in an interpreted language is variable.
Second, don't trust the system too much. What I was seeing between Node versions really should have been a bug in the testing library, or something in my code, or maybe in simple-statistics itself. But in this case, digging deeper revealed that what I was seeing was exactly what you don't expect: a glitch in the language itself.
Third, everyone's winging it. Reading through the V8 implementation gives you a deep appreciation of the genius involved in implementing interpreters, but also an appreciation that it's just humans doing the implementation: they make mistakes, and, as evidenced by the constantly-changing algorithms for mathematics, always have room to improve.
Addendums:
Precision: Commentators on Twitter have pointed out that the variation in example results is outside the significant digits of floating point. This is technically correct, and means that you could potentially come up with a slightly more precise way to compare them than using an epsilon. But practically it's the same story – the trailing digits will propagate into results and create real-world discrepencies. Additionally, the examples I gave aren't exhaustive: JavaScript interpreters can, without cheating the specification, introduce numerical differences in the significant portion of a result.
JavaScript: This isn't a critique of JavaScript. I think that the language made an appropriate compromise in the face of an uncertain future and lots and lots of platforms. And it's really hard to compare any other language directly to JavaScript because the JavaScript ecosystem - lots of different interpreters of the language all coexisting - is pretty darn uncommon, and it's also one of JavaScript's biggest strengths. Also, to be clear, that this is totally different than JavaScript-the-language changing: that's also a thing that's happening, and I'm pretty excited about what's changing in the language.
Stdlib or an epsilon: The practical solution in most cases is using an epsilon. Stdlib is fascinating and powerful, but the cost of including an additional library for mathematics is quite high – and in many cases these small differences in output don't matter for applications.
@macwright.com on Bluesky, @tmcw@mastodon.social on Mastodon